20's Plenty Sheffield
You can help our campaign!
Please email us (to be added to the whatsapp group), or join the group and message us on facebook.
The Problem
300 serious/fatal road collisions happen each year in the city[1] but Sheffield Council policy is based on decades-old research and still specifically excludes main residential roads (even those with schools and shops!!) from being 20mph, even though this is where almost all the serious and fatal collisions occur.The Solution
A default speed of 20mph in Sheffield will massively reduce these injuries - in Edinburgh, a similar scheme reduced serious injuries by 33% across the city[2]. Some roads can still be 30 or 40, but the default for the city should be 20 instead of 30 - this will be cheaper and more effective than the current piecemeal approach. The UN World Health Organisation recommends 20mph where people and cars mix. Default-20mph will also reduce noise and air pollution[3,4] while the reduced speeds lead to more people walking and cycling[5]. Many other cities have done this, e.g. in Bristol, 47% fewer fatal injuries & 16% fewer serious injuries[5].What we're doing
- The council is looking at reviewing the current 20mph strategy. Unfortunately they might be using out-of-date research or "anecdotal" stories to make their decisions. We need to grow our group so it spans the city and puts pressure on councillors to engage with this.
- We are soon going to hold an online meeting between experts from other local authorities who have already done this, and the councillors and transport officers involved here.
- We are also looking to raise public awareness of the benefits of reduced traffic speeds.
How did it start?
The 'founders' are a group of parents of children at Nether Green Infants & Junior schools. The council were putting in a 20mph area but excluding Fulwood Road -- where almost all the serious crashes happen (there's one almost every year within 300m of the two schools!). It turns out the council's own 20mph strategy was blocking them from introducing the lower speed limit. We need to overturn this 'strategy' and make the city safer. This is part of our leafet from that campaign...
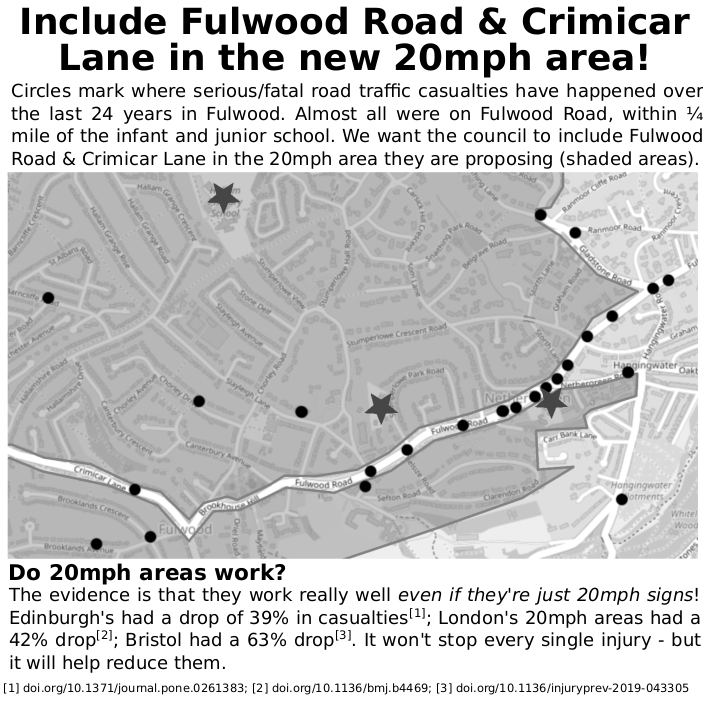 [1] https://sysrp.co.uk/statsarchive [2] https://doi.org/10.1371/journal.pone.0261383; [3] https://doi.org/10.1016/j.envint.2020.106126; [4] Archer, J., et al. "The impact of lowered speed limits in urban and metropolitan areas." (2008); [5] Pilkington, Paul, et al. "The Bristol twenty miles per hour limit evaluation (BRITE) study analysis of the 20mph rollout project." (2018);
[1] https://sysrp.co.uk/statsarchive [2] https://doi.org/10.1371/journal.pone.0261383; [3] https://doi.org/10.1016/j.envint.2020.106126; [4] Archer, J., et al. "The impact of lowered speed limits in urban and metropolitan areas." (2008); [5] Pilkington, Paul, et al. "The Bristol twenty miles per hour limit evaluation (BRITE) study analysis of the 20mph rollout project." (2018);