First, apologies for the pause in blog posts – I’ve been away on shared parental leave for the last few months with my new “project” (aka Samuel :).
Anyway, adversarial examples are now a heavily researched area of machine learning. Modern methods now exist that can successfully classify a test point in high dimensional, highly structured datasets [citation needed, such as images etc]. It has been found however that these successful classification results are susceptible to small perturbations in the location of the test point [e.g. Szegedy et al. 2013]. By carefully crafting the perturbations the attacker can cause an ML classifier to misclassify even with only a tiny perturbation. Many examples exist, from malware detection [Srndic and Laskov, 2014] to vision for autonomous vehicles [Sitawarin et al. 2018].
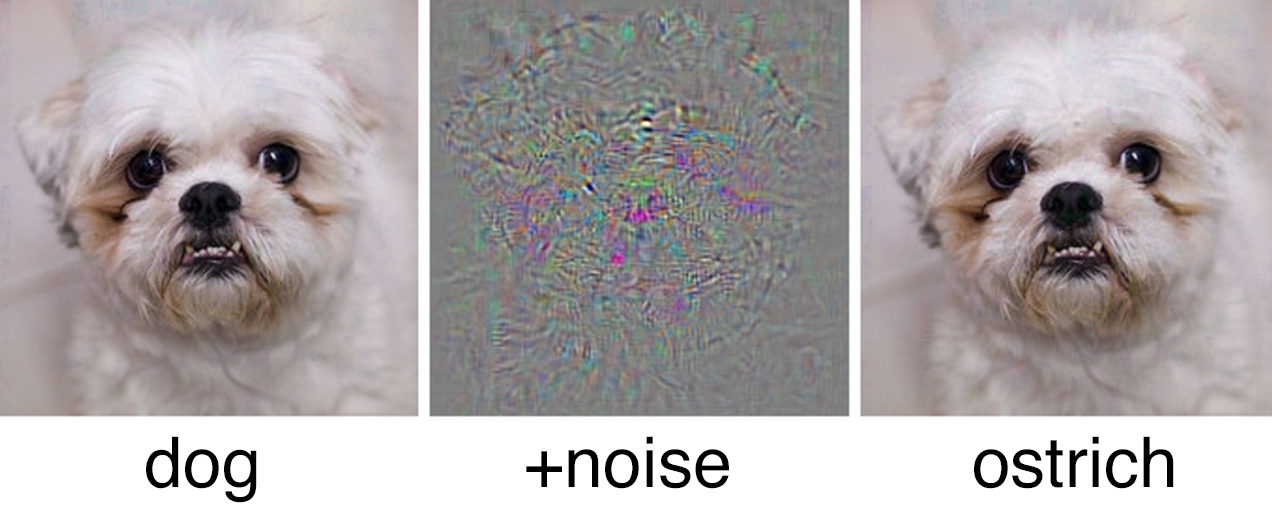
Image from Szegedy, Christian, et al. “Intriguing properties of neural networks.” arXiv preprint arXiv:1312.6199 (2013). Tiny, carefully crafted, changes can cause a misclassification.
Typically in these papers the authors take a correctly classified training point of one class and alter it to become a different class.
A few thoughts on this;
- First, it isn’t clear to me how close to the decision boundary the training points are, one could probably always find real examples that lie very close to the decision boundary and with a tiny tweak could be nudged over the line. I figured that it made more sense to look at examples in which one could move from a highly confident classification of one class to a highly confident classification in another. To motivate with a more practical example, if my self-driving car is only 55% confident the traffic light is green, I’d expect it to stop. It’s what happens if you can move it from 99% confident of a red light to 99% confident of a green.
- Second, deep (convolutional) neural networks struggle with uncertainty – lots of methods have been proposed to try to allow them to quantify that uncertainty a little better, but typically they still seem to do weird things away from where the true training data lies (which is exactly the parts of the domain where adversarial samples lie).
- Third, DNNs have no strong priors about the decision function. To demonstrate if one trains with a low dimensional training set, in which the classes are very separable, the decision boundary provided by the DNN is often close to one of the classes, and is often very sharp.
- A Gaussian process classifier however has strong priors on its latent function, leading to slow changes to the classification. Hence to move between one confident location to another typically requires a large change in the training location.
My collaborators at CISPA (Saarland, Germany) are busy looking at the empirical improvements one can acheive using GPs. I thought it might be interesting to focus on whether one can bound the impact of an adversarial example.
There are typically two ways of generating adversarial examples, the first (illustrated by the dog/ostrich example) involves making small changes to lots of inputs. The second involves modifying a few inputs a lot. In the paper I’m drafting at the moment this is the path I have taken. The question: Can I produce an upper bound on the change in the latent function (or even better in the classification) that changing D inputs could cause?
So for example, if you have a GP classifier distinguishing between two digit image types, how much could the class change if you alter (say) three pixels?
I approached this problem as follows;
- First I restricted the type of kernel to the RBF (EQ) kernel.
- I then consider the change that can occur due to each training input (considering the output as the sum of a set of Gaussians – using the representer theorem).
- I devised a method for bounding the sum of a mixture of Gaussians.
- There’s a bunch of other optimisations etc to achieve a better bound.
Currently I’m just trying this out on some example training data (MNIST!), I suspect that it will only work on low dimensional problems (e.g. less than 20 dimensions) as above that the domain still is too large to search.